不定期更新.author: hos <hos _at_ hos.ac>
C++ の GCC 拡張の __builtin_clz や __builtin_clzll,あるいは Java の Integer.numberOfLeadingZeros や Long.numberOfLeadingZeros は上位のビットにいくつ 0 が並んでいるかを求めてくれます.整数型のサイズ (32 だとか 64 だとか) から引き算することで,log2 n くらいの値が得られますね.
1 つだけ要注意事項として,GCC の場合は引数に 0 を与えたときの結果は undefined です.bsr 命令を使っているからだとかなんとか.手元の Cygwin で試してみたらちゃんととんでもない値になりました.
「log2 n くらい」の「くらい」の詳細は毎回考えていたのですが,わたしはこういうのを考えるのが遅くてストレスを溜めてしまいがちなので,1 回ブログ記事として丁寧に整理してみよう,という試みです.
| n | max{ k ∈ Z | 2k < n } | max{ k ∈ Z | 2k ≤ n } | min{ k ∈ Z | n ≤ 2k } | min{ k ∈ Z | n < 2k } | |
|---|---|---|---|---|---|
| ⌈log2 n⌉ - 1 | ⌊log2 n⌋ | log2 n | ⌈log2 n⌉ | ⌊log2 n⌋ + 1 | |
| size - 1 - clz(n - 1) | size - 1 - clz(n) | size - clz(n - 1) | size - clz(n) | ||
| 0 | -∞* | -∞* | -∞* | -∞* | -∞* |
| 1 | -1* | 0 | 0.00 | 0* | 1 |
| 2 | 0 | 1 | 1.00 | 1 | 2 |
| 3 | 1 | 1 | 1.58 | 2 | 2 |
| 4 | 1 | 2 | 2.00 | 2 | 3 |
| 5 | 2 | 2 | 2.32 | 3 | 3 |
| 6 | 2 | 2 | 2.58 | 3 | 3 |
| 7 | 2 | 2 | 2.81 | 3 | 3 |
| 8 | 2 | 3 | 3.00 | 3 | 4 |
| 9 | 3 | 3 | 3.17 | 4 | 4 |
この表がすべてです.size は 32 だとか 64 だとかです.ここまで書いて初めて size - clz(n) = ⌊log2 n⌋ + 1 を理解しました.
さて,最上段に書いた min とか max とかのやつら,すなわち,n (未満/以下/以上/超過) の (最大/最大/最小/最小) の 2 冪の肩.数学をやるにしてもプログラムを書くにしてもよく使うものですよね.数式で書くなら ⌊log2 n⌋ と ⌈log2 n⌉ で表してしまえばよいわけですが,プログラミングではそれでは使えなくて,clz 関数の登場というわけです.
clz(n) だと丸め方向が ⌊log2 n⌋ 的な方向で固定なので,⌈log2 n⌉ 的なものは clz(n - 1) を呼んでなんとかするわけですが,上の表で clz 系が使えないのは * 印をつけたところです.-∞ があれなのはいいとして,-1 もまだいいとして,⌈log2 1⌉ = 0 を求めようとして死ぬのは衝撃的ですね.clz(2 n - 1) もちょっとやりたくないし,どうするのが綺麗か悩ましいです.
関数 log2 の存在を教えていただきました.少なくとも C++11 なら使えるようです.floor(log(n) / log(2)) みたいな危険極まりないコードを書かずに済むという点が良さそうです.メリットはコードが直感に合うこと.デメリットはパフォーマンスの心配と,double の範囲を超える場合の面倒さですかね.心配事がない状況では (整数に sqrt を使ってしまうくらいの気軽さで) 使っていくのもありかもしれません.
浮動小数点数使うなら frexp はどうか,みたいな指摘が入るかもしれませんが,int k; frexp(n, &k); だなんて不便ですし,これをするなら for 文回したほうがわかりやすいですね.
mod 264 で rolling hash を適当に計算すると,以下の 2 つの文字列のハッシュ値が同じになりませんか? 長さは共に 4096 です.
0110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100101101001100101101001011001101001100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010011001011001101001011010011001011010010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100101101001100101101001011001101001100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100101101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101100110100110010110100101100110100101101001100101101001011001101001100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100101101001100101101001011001101001100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010011001011001101001011010011001011010010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010011001011001101001011010011001011010010110011010010110100110010110011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011010010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010011001011001101001011010011001011010010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100101101001100101101001011001101001100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010011001011001101001011010011001011010010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110 1001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011010010110011010010110100110010110011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101100110100110010110100101100110100101101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011010010110011010010110100110010110011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011010010110011010010110100110010110011010011001011010010110011010010110100110010110100101100110100110010110011010010110100110010110011010011001011010010110011010011001011001101001011010011001011010010110011010010110100110010110011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011010010110011010010110100110010110011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101100110100110010110100101100110100101101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101100110100110010110100101100110100101101001100101101001011001101001100101100110100101101001100101100110100110010110100101100110100110010110011010010110100110010110100101100110100101101001100101100110100110010110100101100110100101101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101100110100110010110100101100110100101101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011010010110011010010110100110010110011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101100110100110010110100101100110100101101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001
Google Code Jam 2014 の決勝に参加してきました.結果は散々でした.
large で不正解をもらった問題 C についてです.そもそも解法がダメで大胆に間違っているのですがそれはおいといて.木の同型判定を含む問題で,その部分はハッシュで実装しようとしました.たとえ多倍長演算でやっていたとしても異なる木が同一の値に対応しうるひどい関数を書いてしまったのもおいといて.木のハッシュをとるなら,適切に Euler tour したときの文字列の rolling hash をとるのが妥当かなと思います.部分木のサイズも一緒に DP しておけば計算できますね.
ところで,恐ろしいことに,ハッシュというものは衝突します.「mod (2 冪) はよくない」という噂を耳にしたことがあって,しかしよく検討したことがなかったので,ちゃんと考えてみました,というのがこの記事です.
整数 b, m を用意して,整数列 s = (s0, s1, ..., sn-1) (si ≠ 0) のハッシュ値を (s0 b0 + s1 b1 + ... + sn-1 bn-1) mod m とします.
とりあえず,中国剰余定理があるので m としては素冪 pk だけ考えればよいです.このとき,常識かと思いますが,b が p の倍数だと悲惨なことになります.sk 以降がハッシュ値に影響しなくなってしまうからですね.また,割り算ができないので数列の平行移動が一方向にしかできなくなります.
さらに,b の mod pk での位数はなるべく大きいほうがよさそうです.もし bi ≡ 1 (mod pk) だったら,例えば j 文字目と i + j 文字目を入れ替えてもハッシュ値に影響しないことになってしまいます.ちなみに mod pk での最大位数は,有名事実ですが,p が奇素数なら φ(pk-1) = pk-1 (p - 1) で,p = 2 については k ≥ 3 のとき φ(2k) / 2 = 2k-2 です.
あとは,b があんまり小さいと数文字で簡単に衝突を起こしてしまってよくない,というのもあるかもしれません.
これくらいの条件を満たしておけば,入力される数列がランダムならなんとかなってるのでは,という気がします.実際にハッシュ値の分布を解析するのはかなり大変そうなのでさぼらせていただきます.が,世の中が回っていることを考えるとたぶん大丈夫です.
今回問題視するのは,入力に悪意がある場合です.もちろん,ハッシュ関数が知られているなら,それが単射になっていない限りは衝突は起こりうるわけで,衝突するデータが投げられる可能性は消せません.一方,例えば GCJ のようなコンテストでは,参加者が使ってくるハッシュ関数は (標準ライブラリのものとかでもない限り) 予想できません.じゃあ,自分だけの秘密の b を選んでおけば衝突する確率は低くできるだろう,と思いがちなのですが,ここに落とし穴があります:高速化あるいは実装の簡略化を考えて m = 264 を選びたくなりますが,そうすると悪意にやられることを以下に示します.
m を (数列の長さと数列の各要素に対して) 十分大きい素数に選んだうえで,b を { 0, 1, ..., m - 1 } から一様ランダムに選びます.これだけで問題ありません.
なぜでしょう.2 つの異なる長さ n の数列 s = (s0, s1, ..., sn-1), s' = (s'0, s'1, ..., s'n-1) のハッシュ値が衝突する確率を考えます (0 詰めなりで長さを揃えておくことにします).このときハッシュが衝突する条件は,s0 b0 + s1 b1 + ... + sn-1 bn-1 ≡ s'0 b0 + s'1 b1 + ... + s'n-1 bn-1 (mod m),すなわち b が Z/mZ 上の多項式 f(X) = (s'0 - s0) X0 + (s'1 - s1) X1 + ... + (s'n-1 - sn-1) Xn-1 の根であることです.m が素数なら Z/mZ は整域ですから,根は高々 n - 1 個.よって,一様ランダムに選んだ b が根となってしまう確率は高々 (n - 1) / m となるのです.
これでおわかりの通り,Z/mZ が整域でないときは,低い次数の f であって根がたくさんあるものが存在する可能性があるわけです.
m = 2k として,任意の奇数が根となる Z/mZ 上の多項式であって,次数が低めのものを構成することを目標とします.
……というと,結構単純に作れます.例えば f(X) = (X - 1)k が条件を満たしますね.これで何が満足いかないかというと,係数が大きいことです.アルファベットからなる文字列でハッシュが衝突するケースは,この多項式からだと作りにくそうです.そういうわけで,係数の絶対値が 1 以下という制約を追加してみようと思います.
よくわからなかったので全探索してみました:
k = 1 X - 1 = (X-1) X + 1 = (X+1) k = 2 X^2 - 1 = (X-1) (X+1) k = 3 X^2 - 1 = (X-1) (X+1) k = 4 X^3 + X^2 - X - 1 = (X-1) (X+1)^2 X^3 - X^2 - X + 1 = (X-1)^2 (X+1) k = 5 X^5 + X^4 - X - 1 = (X-1) (X+1)^2 (X^2+1) X^5 - X^4 - X + 1 = (X-1)^2 (X+1) (X^2+1) k = 6 X^6 - X^4 - X^2 + 1 = (X-1)^2 (X+1)^2 (X^2+1) k = 7 X^6 - X^4 - X^2 + 1 = (X-1)^2 (X+1)^2 (X^2+1) k = 8 X^7 - X^6 - X^5 + X^4 - X^3 + X^2 + X - 1 = (X-1)^3 (X+1)^2 (X^2+1) X^7 + X^6 - X^5 - X^4 - X^3 - X^2 + X + 1 = (X-1)^2 (X+1)^3 (X^2+1) k = 9 X^11 - X^10 - X^9 + X^8 - X^3 + X^2 + X - 1 = (X-1)^3 (X+1)^2 (X^2+1) (X^4+1) X^11 + X^10 - X^9 - X^8 - X^3 - X^2 + X + 1 = (X-1)^2 (X+1)^3 (X^2+1) (X^4+1) k = 10 X^12 - X^10 - X^8 + X^4 + X^2 - 1 = (X-1)^3 (X+1)^3 (X^2+1) (X^2-X+1) (X^2+X+1) k = 11 X^13 + X^12 - X^11 - X^10 - X^9 - X^8 + X^5 + X^4 + X^3 + X^2 - X - 1 = (X+1)^4 (X-1)^3 (X^2+1) (X^2-X+1) (X^2+X+1) X^13 - X^12 - X^11 + X^10 - X^9 + X^8 + X^5 - X^4 + X^3 - X^2 - X + 1 = (X+1)^3 (X-1)^4 (X^2+1) (X^2-X+1) (X^2+X+1) k = 12 X^14 - X^12 - X^10 + X^8 - X^6 + X^4 + X^2 - 1 = (X-1)^3 (X+1)^3 (X^2+1)^2 (X^4+1) k = 13 X^15 + X^14 - X^13 - X^12 - X^11 - X^10 + X^9 + X^8 - X^7 - X^6 + X^5 + X^4 + X^3 + X^2 - X - 1 = (X-1)^3 (X+1)^4 (X^2+1)^2 (X^4+1) X^15 - X^14 - X^13 + X^12 - X^11 + X^10 + X^9 - X^8 - X^7 + X^6 + X^5 - X^4 + X^3 - X^2 - X + 1 = (X-1)^4 (X+1)^3 (X^2+1)^2 (X^4+1)
眺めた結果,X1 - 1, X2 - 1, X4 - 1, X8 - 1, ... からいくつか選んだ積を考えると,係数の絶対値を 1 以下にしつつ根を多く持たせられそうということがわかりました (k = 10 などがある通り,次数最小ではないです).t ≥ 1 に対し,X2t - 1 は 2t+2 で割り切れることに注意します.k = 64 なら,X211 - 1 まで全部かければぴったりですね.最小からは程遠いかもしれないですが,これで 212 - 1 次になります.一般には 2O(k1/2) 次になりますね.
そんな感じで構成したものを文字列にしたのが冒頭の例です.m が 264 の約数なら,どんな奇数を b に選ぼうが衝突します.0 と 1 にどんな整数を割り当てようが衝突することに注意してください.逆から読んでも衝突することにも注意してください.それにしても,i 文字目 (0-based) は i の立っているビットの個数の偶奇で決まっているという,如何にもありそうな文字列であるのがまたなんとも言えないですね.
mod (2 冪) はやめましょう.
mod (素数) で何通りか計算することにして,例えば長さ 106 くらいの文字列を 106 組くらい比較するなら,109 くらいの素数を 3 つ用意してようやく,どんな悪意に満ちた入力が来ても 99.9% 安心,という評価ができます.結構大変.もっといい評価あったら教えてください.
想定解がハッシュな問題を作る方は,ある程度安心できるハッシュは実行時間が結構かかるということにどうかご留意ください.
Yandex.Algorithm 2014 の決勝に参加してきました.結果は 2 位.いつも通りの負け方で残念でなりません.
さて,提出を blind で攻めるとすると,一発で通さなければならないので計算量に自信がない解法は避けたくなります.コンテスト本番で,こんな状況になりました:「たくさんの文字列をソートしたい.長さの合計が 2,000,000 以下.」時間制限は 4 秒.実際はさらに index とペアにしてソートです.これを C++ の std::sort に投げられるでしょうか.わたしは計算量に自信が持てず,安全性が把握できる trie を用いることを選びました.
長さ x の文字列と長さ y の文字列の比較にかかる時間を O(min{x, y}) とします.長さの合計を L として,均等に長さ L1/2 の文字列が L1/2 個なら,std::sort で O(L log L) 時間が保証され (最悪計算量の保証は C++11 からだそうですが),問題ありません.均等でないときも計算量の上限が見積もれるだろうか?が今回のテーマです.
C++ の規格書として何を読めばいいのか詳しくないのですが,N3337 を見てみると,比較が O(N log N) 回 (N は配列の長さ) としか書いていません.これではちょっとあんまり.cplusplus.com には swap あるいは move の回数もそれで抑えられると書かれています.
いずれにせよ,これでは長い文字列をひたすら選ぶどうしようもない実装になっていたらどうしようもありません.
std::sort は大抵 introsort で実装されているだろうと信じて,その検討をしてみることにします.読んだコードは g++ 4.8.2 (Ubuntu 14.04) の stl_algo.h です.
まずは quicksort フェーズ.最大で 2 log N 回くらいの再帰をするようです.各段階では,まず __first + 1, __first + (__last - __first) / 2, __last - 1 の median を pivot として先頭に移動させ (最大 3 回比較,1 回 swap),pivot 以下と pivot 以上になるように分割しています (pivot と各要素を最大 2 回ずつ比較,各要素最大 1 回ずつ swap).ということで計算量は各段階で O(L) になっています.
続いて heap sort フェーズ.……は実装をちゃんと読んでいないのですが,まあ heap sort なので,各要素がせいぜい昇って降りて昇るだけで済むので O(L log N) 時間です.ちなみに,std::partial_sort に渡される実装になっています.
あとはおまけ的に insertion sort をする箇所がありますが,線型 (のはず) です.というわけで,大丈夫そうなことがわかりました.
普通の (in-place でない) merge sort を考えてみます.2 つの列を merge するとき,先頭を比較して 1 つずつ pop していくわけですが,比較の計算量は pop されるほうの長さで抑えられます.これに外部記憶の読み書きを合わせても,きっかりデータサイズ.再帰の深さは log N で済むので,最悪計算量は O(L log N) です.
std::stable_sort は大抵 merge sort で実装されていると信じています.実装を見てみたら,長さ 15 未満で insertion sort に切り替えていました.
quicksort フェーズが悲しいことになる入力って,案外単純に作れるんですね.知りませんでした.というわけで作ってみました.
手元での実行結果 (要素数 1,000,000):
copyctor movector copy= move= swap compare 0 5496822 0 22421385 1153 59276139 std::sort 0 4499997 0 21392093 0 20242748 std::partial_sort 0 1857142 0 21080888 0 19516290 std::stable_sort 0 19951424 0 29591496 0 18365967 MergeSort (自前,std::inplace_merge を借用)
作り方は,0,0, 1,1,1, 2,2,2,2, 3,3,3,3,3, ..., 3, 2, 1, 0 という具合です.std::sort のパフォーマンスはちゃんと酷くなりました.std::partial_sort は演算回数だけ見ると悪くなさそうですが,ご存知の通りメモリアクセスが悲惨なので遅いです.
自前の merge sort は move の回数が多いですね.move のコストが大きい場合はポインタをソートするようにするメリットが大きいかもしれません.std::unique_ptr とかのおかげでそういうのもやりやすくなったと思います.
ラッパーを除いて実行時間も測ってみました (要素数 1,000,000,文字列の長さすべて 2).順に ideone / Yandex.Algorithm / 手元 です.
| std::sort | std::partial_sort | std::stable_sort | MergeSort |
|---|---|---|---|
| 1.97s / 1.28s / 1.04s | 1.33s / 0.99s / 0.82s | 1.25s / 0.85s / 0.51s | 1.46s / 0.69s / 0.50s |
結構怖いですね.
※ 特に C++ に関して,怪しかったらご指摘ください.
和一定の下で std::sort は適切.ただし merge sort の存在を忘れるべからず.
この記事は,Competitive Programming Advent Calendar の第 19 日目として書かれました.
priority queue (優先度付きキュー) を実現するデータ構造について紹介してみます.
priority queue ってなんでしょう? ご存知の方も多いと思いますが,
という操作を効率良く行うものを指します.お店に人が並んでいて,「人を追加する」「予約時刻が最も早い人を中に入れる」みたいなイメージですね.「効率良く」と書きましたが,priority queue 内の要素数を n として,1 操作あたり O(log n) の効率がほしいところです.もちろん,「最小」の代わりに「最大」を考えることもあります.また,最小の値にアクセスする (取り除きはしない) という操作を O(1) 時間で行えることを要求する場合も多いです.
ところで,世の中には平衡二分探索木というデータ構造があり,追加や削除や検索を含めて各操作を O(log n) で処理できます.それでは priority queue はただの下位互換かというとそうではなくて,機能が制限されたことによる構造の単純さ,それに伴う定数倍の高速化というメリットがあります.この定数倍はかなり大きいものです.
ではどうやってデータを保持するか? ということですが,お馴染みのデータ構造である木 (根付き木) を用いるのが基本となります.各ノードが 1 つの要素を表しますが,heap-order property と呼ばれる以下の性質を満たすようにします:
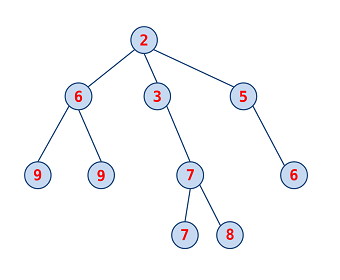
この条件により,最小値は常に根に来るため,容易にアクセスできます.一方,子ノードたちの大小関係には制約がないため,部分木の位置を入れ替えるという操作が可能であり,これは後半の話の鍵となります.なお,今回紹介するヒープはすべて二分木です.
binary heap (二分ヒープ) は,ヒープが常に完全二分木の形を保つようにして管理するものです.おそらく最も良く知られた構造でしょう.資料は世に溢れていると思うので,この記事では詳細な説明を省略します.
binary heap は priority queue としての基本的な機能しか持たないのですが,ちょっと違った方針でデータ構造を考えることで追加機能を持たせられる,というのが今回のメインテーマになります.
leftist heap (あるいは leftist tree) は,通常の priority queue の機能に加え,
という操作を効率良く行えるデータ構造です.お店の例で言えば「待っている人たちが 2 箇所にばらけてしまったので合体させよう」というのにあたるでしょうか.この一見あまり使いどころが多くなさそうな機能ですが,
というように,push や pop という操作は meld 操作を使って言い換えることができます.
この meld 操作の実現方法は,leftist heap の擬似コードを見てしまうのが手っ取り早いでしょう.
class Heap { Heap l, r; int s; T val; } Heap meld(Heap a, Heap b) { if (a is null) return b; if (b is null) return a; if (a.val > b.val) swap(a, b); a.r = meld(a.r, b); if (a.l is null || a.l.s < a.r.s) swap(a.l, a.r); a.s = ((a.r is null) ? 0 : a.r.s) + 1; return a; }
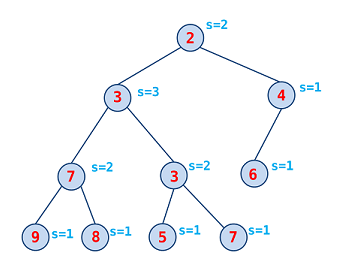
各ノードは,左右の子へのポインタ,自身の値の他に,s という値を持っています.これは子を辿っていって null に着くまでの最小回数を表します.そして leftist heap という名の通り,木が左に偏っている,すなわち
という条件が常に保たれるようにします.すると,meld は 2 つのヒープの最右パスをマージするような動作をしますが,条件により最右パスの長さは log (ノード数) を超えないので,各操作を対数時間で行えることがわかります.
続いて,私が好きなデータ構造の 1 つでもある skew heap を紹介します.早速コードを見てみることにしましょう.
class Heap { Heap l, r; T val; } Heap meld(Heap a, Heap b) { if (a is null) return b; if (b is null) return a; if (a.val > b.val) swap(a, b); a.r = meld(a.r, b); swap(a.l, a.r); return a; }
なんと,leftist heap から s に関する部分がさっぱりなくなってしまっただけです.こんなので本当にうまくいくのかという感じですが,実際にヒープの最も右のパスの長さは非常に長くなりえます.というわけで,1 回の操作を対数時間で行えない可能性があります.しかし,ならし計算量を考えると 1 操作あたりのコストは O(log (ノード数)) となることが示せます.以下に証明の概略を記します.
根でないノード u に対して,その親ノードを p として,u が p の左の子であるとき u は left であるといい,右の子であるとき right であるということにします.また,
を満たすとき u は heavy であるといい,そうでないとき light であるということにします.根からのあるパス上には light なノードは高々 log (ヒープ全体のノード数) 個しか含まれないことに注意します.ヒープの集合に対して,そのポテンシャルを right heavy なノードの個数として定義します.ノード数 n1, n2 の 2 つのヒープを meld する操作を考えるとき,実際のコストは最右パス上のノード数の和と考えることができます.各ヒープの最右パス上の heavy なノード数を h1, h2 とするとき,
がわかります.ここで,meld によって h1 + h2 個の right heavy なノードが left となりますが,新たに right heavy なノードが生まれるかもしれません.しかしそれらは,新しいヒープの最左パス上の light なノードと対応することがわかるので,
となります.よって,
であり,ポテンシャルが初期値 0 の非負値をとることと合わせて,示したいことが得られました.
skew heap のメリットとして,木の形に制限がないという点があります.このことを生かすと,根以外のノードであってもそこで親ノードと切り離して取り出してくることで削除できます (その後 meld によって再び 1 つのヒープにできる).実装上は,親ノードへのポインタが必要になるため meld の処理が数行増えます.気になるのはこの操作の計算量ですが,先程と同様に解析できます.操作の実際のコストは定数であり,ノード u を切り離したときに増加する heavy なノードは,新しいヒープの根から u の親ノードまでのパス上の light なノードに対応するため,ポテンシャルの増加は高々 log (ノード数) であり,amortized で対数時間であることが従います.
同様に,あるノードの持つ値を減少させることもできます (値を減らして,heap-order property を満たさなかったら切り離して meld する).これは例えば Dijkstra のアルゴリズムに応用でき,priority queue のメモリを O(グラフの頂点数) に抑えることができます.なお,値を減少させる操作を定数時間 (amortized) で行う priority queue として,Fibonacci heap が知られています.
leftist heap や skew heap の利用価値ははたしてあるのか,というところは,ここを読んでいる方にとっては最も興味があるところかもしれません.上で挙げた Dijkstra のメモリ節約は,グラフを陽に持った時点で O(グラフの辺数) のメモリを使ってしまうので,あまりお目にかかる機会はないかもしれません.他に役立つ可能性がある機会は次のようなところでしょうか:
1 つ目については,私は最適平衡二分木を求める Hu-Tucker のアルゴリズムの実装に用いられることしか知りません.POJ 1738 が検証に使えます (が,この問題ではデータの癖により Garcia-Wachs のアルゴリズムを手抜き + 枝刈りで組むのが早いとかなんとかだそうで).2 つ目は未検証です.データの特性やメモリ確保の方法などにもよると思うので測定が難しい気がしています.経験的には,極端に遅いということは少なくともないです.良さそうなデータがわかったら教えてください.3 つ目も,C++ や Java を使う限りではどうでもいいですが,skew heap の簡潔な実装を見てしまった今では,ぱっと自前の priority queue を書きたいときに二分ヒープを実装する気にはもはやなれないのではないでしょうか.
丁寧な説明をところどころ省いており不親切な記事になってしまったかもしれませんが,調べる際の手がかりくらいにはなるかな,と思います.この記事の狙いの 1 つとして,コンテストで meldable priority queue がほしくなる問題が増えるといいな,という思いを込めていました (普段問題を作っている皆さんぜひお願いします).ともあれ,こんな感じの話題にちょっとでも興味を持っていただけたら幸いです.